2020年數(shù)學(xué)學(xué)習(xí)方法：四邊形的“性質(zhì)與判定”

　　一、四邊形的“一般與特殊”

 

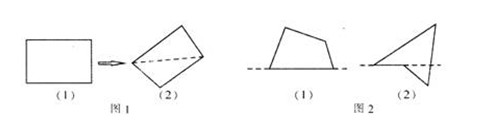
　　在幾何中，四邊形的一般定義為：四條首尾相接的線段組成的圖形叫做四邊形.組成四邊形的四條線段.叫做四邊形的四條邊.按照四條邊是否共面，可以把四邊形分為兩類：四條邊在同一平面內(nèi)的四邊形叫做平面四邊形;四條邊不在同一平面內(nèi)的四邊形叫做空間四邊形.例如，把一張方形的紙鋪平，它的四邊就組成一個(gè)平面四邊形;把這張紙沿對(duì)角線折一下，使對(duì)角線兩旁的部分不在同一平面內(nèi)，這張紙的四條邊就組成了一個(gè)空間四邊形(如圖1).初中數(shù)學(xué)中主要討論平面四邊形.

 

　　平面四邊形又可以進(jìn)一步分為兩類：畫出平面四邊形的任意一條邊所在直線時(shí)，如果整個(gè)四邊形都在直線的同側(cè)，則它是凸四邊形(如圖2(1));否則它是凹四邊形(如圖2(2)).初中數(shù)學(xué)中討論的四邊形主要是凸四邊形.

 

　　四邊形的“一般與特殊”，“性質(zhì)與判定”

 

 

　　對(duì)于一般的四邊形，四條邊只要能夠首尾相接即可，并：無其他關(guān)于邊的位置或長(zhǎng)短的要求.梯形、平行四邊形、矩形、菱形、正方形則不僅都是四邊形，并且各自滿足一定的附加條件.像這樣滿足一定附加條件的四邊形稱為特殊的四邊形.進(jìn)一步可以看出，矩形、菱形和正方形又是滿足一定附加條件的平行四邊形，即它們是特殊的平行四邊形.

 

　　二、四邊形的“性質(zhì)與判定”

 

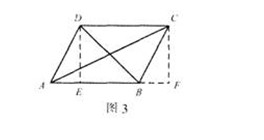
　　通常，教科書中在給出一種圖形的定義后，會(huì)繼續(xù)討論由這個(gè)定義能進(jìn)一步推出哪些結(jié)論，即得出這種圖形的一些性質(zhì).這些性質(zhì)往往是經(jīng)常用到的主要性質(zhì).這種圖形很可能還有一些其他性質(zhì)，教科書則未曾涉及.例如，平行四邊形除具有教科書中所說的“對(duì)邊平行且相等”“對(duì)角相等”“對(duì)角線互相平分”等主要性質(zhì)之外，還有“對(duì)角線的平方和等于四條邊的平方和”這個(gè)性質(zhì).它可以證明如下.

 

　　如圖3，作ABCD的高線DE，CF.利用全等三角形可以證明AE=BF.

 

　　AC2=AF2+CF2=(AB+BF)2+BC2-BF2=AB2+BC2+2AB·BF，

 

　　BD2=BE2+DE2=(AB-AE)2+DA2-AE2=AB2+DA2-2AB·AE。

 

　　∵AB=CD，AE=BF，

 

　　∴①+②，得AC2+BD2=AB2+BC2+CD2+DA2。

 

 

　　四邊形的“一般與特殊”，“性質(zhì)與判定”

 

　　實(shí)際上，圖形的所有性質(zhì)都是由圖形定義所確定的.雖然定義本身并未直接表述出所有性質(zhì)，但是定義中已經(jīng)隱含了它們.故而以定義為出發(fā)點(diǎn)，可以逐步推導(dǎo)出所有性質(zhì).

 

　　圖形的“性質(zhì)”和“判定”，是兩類不同的問題.討論一種圖形的性質(zhì)，是在確定對(duì)象已經(jīng)是這種圖形的前提下進(jìn)行的;討論一種圖形的判定，是為確定對(duì)象是這種圖形而進(jìn)行的.有時(shí)，在分析某個(gè)問題的過程中，兩類問題都會(huì)出現(xiàn)，如先判定某對(duì)象是一種特定的圖形.再推導(dǎo)出它的一些性質(zhì).

 

　　是不是只要一種圖形有某條性質(zhì)，就可以反過來把這條性質(zhì)當(dāng)成這種圖形的一個(gè)判定條件呢?不是!并非一種圖形的每個(gè)性質(zhì)都可以拿來作為這種圖形的判定條件.例如，正方形具有“對(duì)邊平行，鄰邊相等”的性質(zhì)，但是僅根據(jù)一個(gè)四邊形滿足“對(duì)邊平行.鄰邊相等”不能判定它是正方形，而只能判定它是菱形.

 

　　然而，“對(duì)邊平行，鄰邊相等.鄰角相等”是正方形所獨(dú)有的性質(zhì)，因此它能作為正方形的判定條件.又如，矩形具有“對(duì)角線相等”的性質(zhì)，但是僅根據(jù)一個(gè)四邊形的“對(duì)角線相等”并不能判定這個(gè)四邊形是矩形.

 

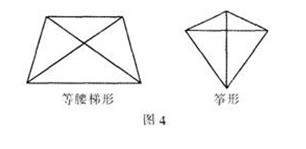
　　圖4中的等腰梯形和箏形都是對(duì)角線相等的四邊形，但它們不是矩形.如果一個(gè)四邊形“對(duì)角線相等”且“對(duì)邊平行”，則它一定是矩形，即一個(gè)四邊形“對(duì)邊平行，對(duì)角線相等”可以作為矩形的一個(gè)判定條件.總之，一種圖形的判定條件，必須是只有這種圖形才能夠滿足的條件.

 

 

　　四邊形的“一般與特殊”，“性質(zhì)與判定”