已知:如下圖,A����、B兩點(diǎn)是直線l同旁的兩個(gè)定點(diǎn)
問(wèn)題:在直線l上求一點(diǎn)P,使得PA+PB的值最小.
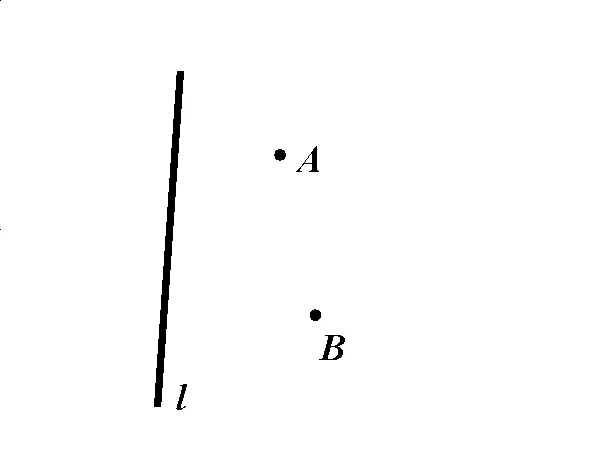
分析:作點(diǎn)A關(guān)于直線l的對(duì)稱點(diǎn)A’���,連結(jié)A’B,交直線于點(diǎn)P����,此時(shí)PA+PB=A’B最小.證明過(guò)程很簡(jiǎn)單,在直線上再任取一點(diǎn)P’���,P’A=P’A’�,P’A+P’B=P’A’+P’B>A’B,所以點(diǎn)P是所求.
模型應(yīng)用:
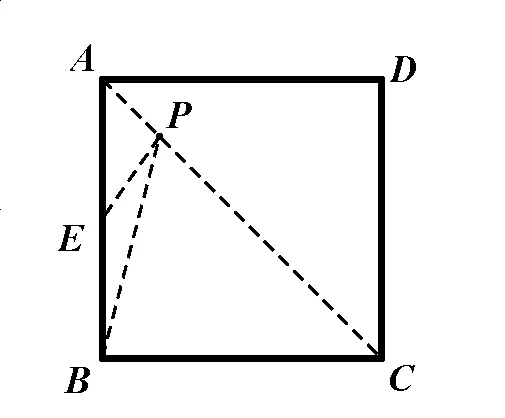
(1)如圖�����,正方形ABCD邊長(zhǎng)為2�,點(diǎn)E是邊AB中點(diǎn),點(diǎn)P是對(duì)角線AC上一點(diǎn).則PE+PB的最小值是 .
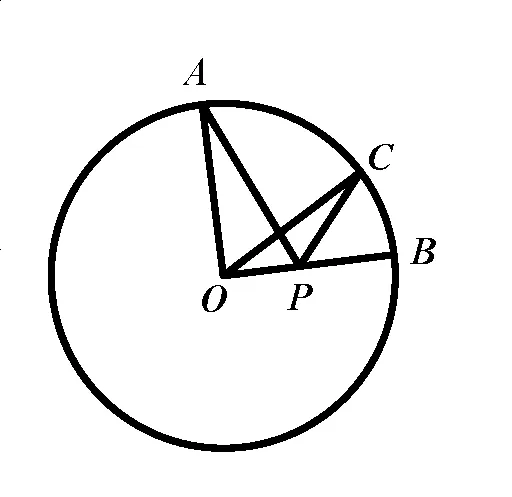
(2)如圖��,⊙O的半徑為2�,點(diǎn)A、B��、C在⊙O上�,OA⊥OB,∠AOC=60°�����,P是OB上一點(diǎn)���,則PA+PC的最小值是 .
(3)如圖���,直線AB與x軸交于點(diǎn)A(2,0)�����,與y軸交于點(diǎn)B(0,4)����,點(diǎn)C、D分別是OA���、AB的中點(diǎn)����,P是OB上一點(diǎn)���,求△PCD周長(zhǎng)的最小值.
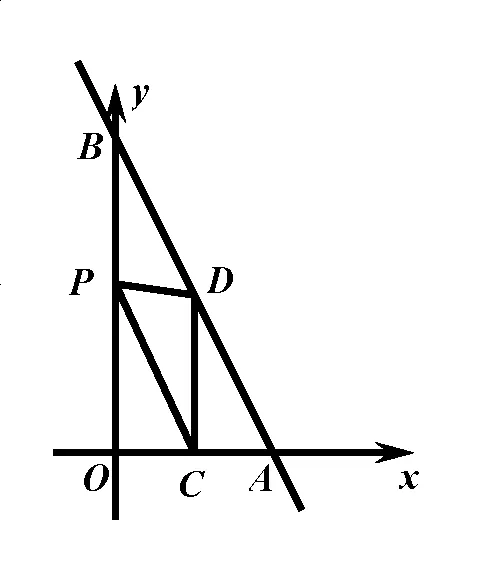
以上幾題是模型1在不同題型中的運(yùn)用�,同學(xué)們?nèi)绻芫毘?ldquo;火眼金睛”��,善于在變化的條件中找到不變的數(shù)學(xué)模型��,“以不變應(yīng)萬(wàn)變”��,就可以像孫悟空一樣成為考場(chǎng)上的“斗戰(zhàn)勝佛”.如果把模型1中的條件稍作調(diào)整����,又可以得到它的一些推廣模型.
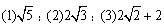
答案:
推廣1:
已知:如圖��,點(diǎn)P是∠AOB內(nèi)一定點(diǎn).
問(wèn)題:分別在OA�����、OB邊上找點(diǎn)M���、N,使△PMN的周長(zhǎng)最小.
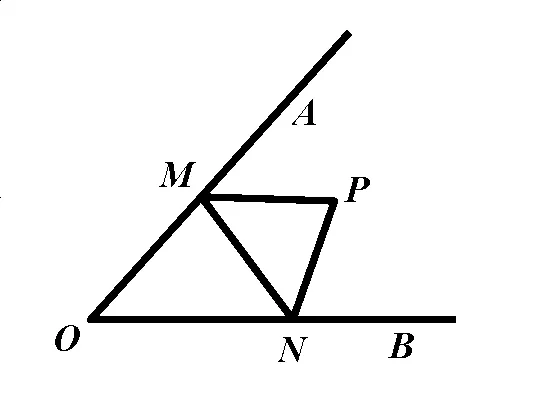
分析:△PMN的周長(zhǎng)=PM+MN+NP�,可以利用作軸對(duì)稱,把這三條線段轉(zhuǎn)化為同一直線上的線段.如圖��,分別作點(diǎn)P關(guān)于OA����、OB的對(duì)稱點(diǎn)P’、P’’�,連結(jié)P’P’’,分別交OA�����、OB于點(diǎn)M���、N����,連結(jié)PM、PN���,此時(shí)PM=P’M�,PN=P’N��,△PMN的周長(zhǎng)=PM+MN+NP=P’P’’����,此時(shí)周長(zhǎng)最小.
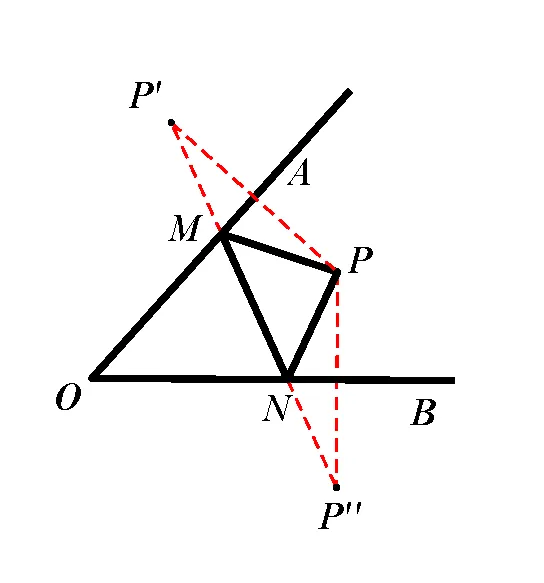
模型應(yīng)用:如圖�����,點(diǎn)C(1,0)����,直線y=-x+7與兩坐標(biāo)軸分別交于A、B兩點(diǎn)��,D����、E分別是AB����、OA上的動(dòng)點(diǎn)�,則△CDE周長(zhǎng)的最小值是
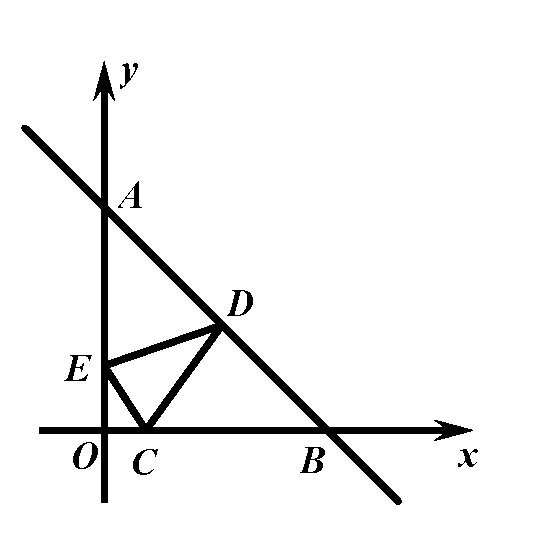
.
答案:10
推廣2:
已知:點(diǎn)P、Q是∠AOB內(nèi)部?jī)啥c(diǎn).
問(wèn)題:分別在直線OA�����、OB上找點(diǎn)M���、N����,使四邊形PMNQ的周長(zhǎng)最小.
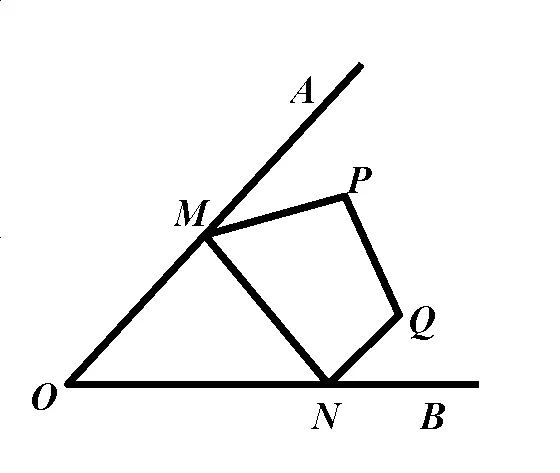
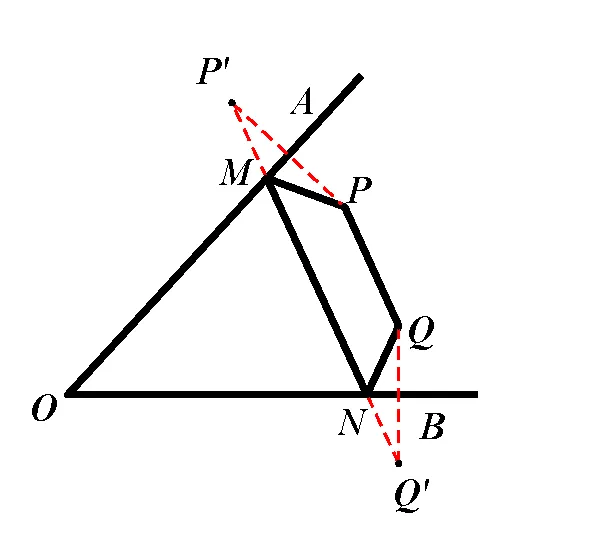
分析:因?yàn)镻Q的長(zhǎng)度是定值����,要使四邊形PMNQ的周長(zhǎng)最小,就是要使PM+MN+NQ的值最小.作點(diǎn)P關(guān)于OA的對(duì)稱點(diǎn)P’�����,作點(diǎn)Q關(guān)于OB的對(duì)稱點(diǎn)Q’�����,連結(jié)P’Q’,分別交直線OA��、OB于點(diǎn)M�����、N���,連結(jié)PM�����、MN、NQ��,因?yàn)镻M=P’M����,QN=Q’N,所以四邊形PMNQ的周長(zhǎng)=PM+MN+NQ+QP=P’Q’+PQ�����,因?yàn)镻Q是定值����,而PM+MN+NQ的最小值為P’Q’的長(zhǎng)度�,所以此時(shí)四邊形PMNQ的周長(zhǎng)最小.
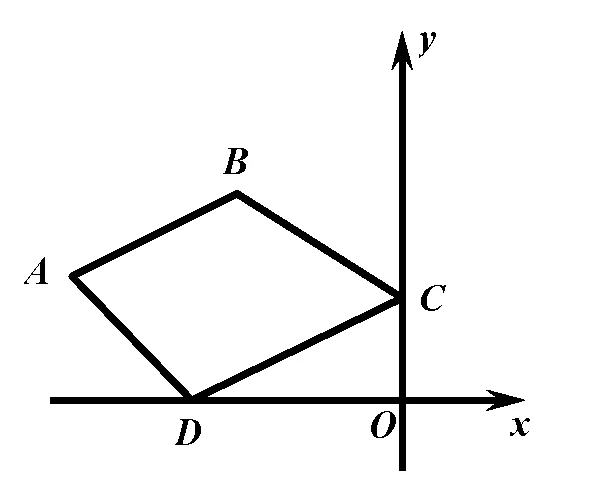
模型應(yīng)用:在平面直角坐標(biāo)系中�����,點(diǎn)A(-8,3)�,點(diǎn)B(-4,5),點(diǎn)C(0����,n),點(diǎn)D(m�,0),當(dāng)四邊形ABCD周長(zhǎng)最短時(shí)���,求m:n的值.
答案:
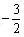
在變化萬(wàn)千的已知條件下���,能夠找到不變的規(guī)律,這與《易經(jīng)》中闡述的“變與不變”的智慧相吻合.人類最高的智慧���,就是“以不變應(yīng)萬(wàn)變”���,這也是數(shù)學(xué)學(xué)習(xí)的無(wú)敵法寶.
相關(guān)推薦:
2022年中考各科目重點(diǎn)知識(shí)匯總
關(guān)注中考網(wǎng)微信公眾號(hào)
每日推送中考知識(shí)點(diǎn)��,應(yīng)試技巧
助你迎接2022年中考��!

歡迎使用手機(jī)�、平板等移動(dòng)設(shè)備訪問(wèn)中考網(wǎng)���,2023中考一路陪伴同行����!>>點(diǎn)擊查看










