ę╗�ĪółAĄ─ėąĻP(gu©Īn)Ė┼─Ņ
1.┼cłAėąĻP(gu©Īn)Ą─Ė┼─Ņ║═ąį┘|(zh©¼)
1)łAŻ║ŲĮ├µ╔ŽĄĮČ©³cĄ─ŠÓļxĄ╚ė┌Č©ķLĄ─╦∙ėą³cĮM│╔Ą─łDą╬.
2)Žę┼cų▒ÅĮŻ║▀BĮėłA╔Ž╚╬ęŌā╔³cĄ─ŠĆČ╬Įąū÷Žę����Ż¼▀^łAą─Ą─ŽęĮąū÷ų▒ÅĮŻ¼ų▒ÅĮ╩ŪłAā╚(n©©i)ūŅķLĄ─Žę.
3)╗����ĪŻ║łA╔Ž╚╬ęŌā╔³cķgĄ─▓┐ĘųĮąū÷╗ĪŻ¼ąĪė┌░ļłAĄ─╗ĪĮąū÷┴ė╗Ī����Ż¼┤¾ė┌░ļłAĄ─╗ĪĮąū÷ā×(y©Łu)╗Ī.
4)łAą─ĮŪŻ║Ēö³cį┌łAą─Ą─ĮŪĮąū÷łAą─ĮŪ.
5)łAų▄ĮŪŻ║Ēö³cį┌łA╔Ž����Ż¼▓óŪęā╔▀ģČ╝┼cłA▀Ćėąę╗éĆĮ╗³cĄ─ĮŪĮąū÷łAų▄ĮŪ.
6)Žęą─ŠÓŻ║łAą─ĄĮŽęĄ─ŠÓļx.
2.ūóęŌ
1)Įø(j©®ng)▀^łAą─Ą─ų▒ŠĆ╩ŪįōłAĄ─ī”ĘQ▌S���Ż¼╣╩łAĄ─ī”ĘQ▌Sėą¤oöĄ(sh©┤)Śl;
2)3³c┤_Č©ę╗éĆłA��Ż¼Įø(j©®ng)▀^1³c╗“2³cĄ─łAėą¤oöĄ(sh©┤)éĆ.
3)╚╬ęŌ╚²ĮŪą╬Ą─╚²éĆĒö³c┤_Č©ę╗éĆłAŻ¼╝┤įō╚²ĮŪą╬Ą─═ŌĮėłA.
Č■�����Īó┤╣ÅĮČ©└Ē╝░Ųõ═Ųšō
1.┤╣ÅĮČ©└ĒŻ║┤╣ų▒ė┌ŽęĄ─ų▒ÅĮŲĮĘų▀@ŚlŽę��Ż¼▓óŪęŲĮĘųŽę╦∙ī”Ą─ā╔Śl╗Ī.
ĻP(gu©Īn)ė┌┤╣ÅĮČ©└ĒĄ─ėŗ╦Ń│Ż┼c╣┤╣╔Č©└ĒŽÓĮY(ji©”)║Ž���Ż¼ĮŌŅ}Ģr═∙═∙ąĶę¬╠Ē╝ė▌oų·ŠĆ�Ż¼ę╗░Ń▀^łAą─ū„ŽęĄ─┤╣ŠĆ����Ż¼śŗ(g©░u)įņų▒ĮŪ╚²ĮŪą╬.
2.═Ųšō
1)ŲĮĘųŽę(▓╗╩Ūų▒ÅĮ)Ą─ų▒ÅĮ┤╣ų▒ė┌ŽęŻ¼▓óŪęŲĮĘųŽę╦∙ī”Ą─ā╔Śl╗Ī;
2)ŽęĄ─┤╣ų▒ŲĮĘųŠĆĮø(j©®ng)▀^łAą─��Ż¼▓óŪęŲĮĘųŽę╦∙ī”Ą─ā╔Śl╗Ī.
╚²���ĪółAą─ĮŪ�Īó╗ĪĪóŽęĄ─ĻP(gu©Īn)ŽĄ
1.Č©└ĒŻ║į┌═¼łA╗“Ą╚łAųą�����Ż¼ŽÓĄ╚Ą─łAą─ĮŪ╦∙ī”Ą─╗ĪŽÓĄ╚�Ż¼╦∙ī”Ą─ŽęŽÓĄ╚.łAą─ĮŪĪó╗Ī║═Žęų«ķgĄ─Ą╚┴┐ĻP(gu©Īn)ŽĄ▒žĒÜį┌═¼łAĄ╚╩Įųą▓┼│╔┴ó.
2.═ŲšōŻ║į┌═¼łA╗“Ą╚łAųą����Ż¼╚ń╣¹ā╔éĆłAą─ĮŪĪóā╔Śl╗Ī��Īóā╔ŚlŽęųąėąę╗ĮM┴┐ŽÓĄ╚���Ż¼─Ū├┤╦³éā╦∙ī”æ¬(y©®ng)Ą─ŲõėÓĖ„ĮM┴┐Č╝ĘųäeŽÓĄ╚.
╦─���ĪółAų▄ĮŪČ©└Ē╝░Ųõ═Ųšō
1.Č©└ĒŻ║ę╗Śl╗Ī╦∙ī”Ą─łAų▄ĮŪĄ╚ė┌╦³╦∙ī”Ą─łAą─ĮŪĄ─ę╗░ļ.
2.═ŲšōŻ║1)į┌═¼łA╗“Ą╚łAųąŻ¼═¼╗Ī╗“Ą╚╗Ī╦∙ī”Ą─łAų▄ĮŪŽÓĄ╚. 2)ų▒ÅĮ╦∙ī”Ą─łAų▄ĮŪ╩Ūų▒ĮŪ.
łAā╚(n©©i)Įė╦─▀ģą╬Ą─ī”ĮŪ╗źča.į┌łAųąŪ¾ĮŪČ╚Ģr�����Ż¼═©│ŻąĶę¬═©▀^ę╗ą®łAĄ─ąį┘|(zh©¼)▀Mąą▐D(zhu©Żn)╗».▒╚╚ńłAą─ĮŪ┼cłAų▄ĮŪķgĄ─▐D(zhu©Żn)╗»;═¼╗Ī╗“Ą╚╗ĪĄ─łAų▄ĮŪķgĄ─▐D(zhu©Żn)╗»;▀Bų▒ÅĮŻ¼Ą├ĄĮų▒ĮŪ╚²ĮŪą╬���Ż¼═©▀^ā╔õJĮŪ╗źėÓ▀Mąą▐D(zhu©Żn)╗»Ą╚.
╬Õ�����Īó┼cłAėąĻP(gu©Īn)Ą─╬╗ų├ĻP(gu©Īn)ŽĄ
1.³c┼cłAĄ─╬╗ų├ĻP(gu©Īn)ŽĄ
įO(sh©©)³cĄĮłAą─Ą─ŠÓļx×ķd.
(1)d
(2)d=r⇔³cį┌ĪčO╔Ž;
(3)d>r⇔³cį┌ĪčO═Ō.
┼ąöÓ³c┼cłAų«ķgĄ─╬╗ų├ĻP(gu©Īn)ŽĄ���Ż¼īóįō³cĄ─łAą─ŠÓ┼c░ļÅĮū„▒╚▌^╝┤┐╔.
2.ų▒ŠĆ║═łAĄ─╬╗ų├ĻP(gu©Īn)ŽĄ
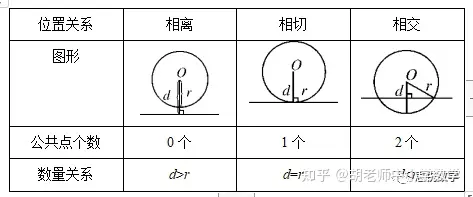
ė╔ė┌łA╩Ū▌Sī”ĘQ║═ųąą─ī”ĘQłDą╬Ż¼╦∙ęįĻP(gu©Īn)ė┌łAĄ─╬╗ų├╗“ėŗ╦ŃŅ}ųą│Ż│Ż│÷¼F(xi©żn)ĘųŅÉėæšōČÓĮŌĄ─Ūķør.
┴∙�����ĪóŪąŠĆĄ─ąį┘|(zh©¼)┼c┼ąČ©
1.ŪąŠĆĄ─ąį┘|(zh©¼)
1)ŪąŠĆ┼cłAų╗ėąę╗éĆ╣½╣▓³c.2)ŪąŠĆĄĮłAą─Ą─ŠÓļxĄ╚ė┌łAĄ─░ļÅĮ.3)ŪąŠĆ┤╣ų▒ė┌Įø(j©®ng)▀^Ūą³cĄ─░ļÅĮ.
└¹ė├ŪąŠĆĄ─ąį┘|(zh©¼)ĮŌøQå¢Ņ}Ģr�����Ż¼═©│Ż▀B▀^Ūą³cĄ─░ļÅĮ�����Ż¼└¹ė├ų▒ĮŪ╚²ĮŪą╬Ą─ąį┘|(zh©¼)üĒĮŌøQå¢Ņ}.
2.ŪąŠĆĄ─┼ąČ©
1)┼cłAų╗ėąę╗éĆ╣½╣▓³cĄ─ų▒ŠĆ╩ŪłAĄ─ŪąŠĆ(Č©┴xĘ©).
2)ĄĮłAą─Ą─ŠÓļxĄ╚ė┌░ļÅĮĄ─ų▒ŠĆ╩ŪłAĄ─ŪąŠĆ.
3)Įø(j©®ng)▀^░ļÅĮ═ŌČ╦³c▓óŪę┤╣ų▒ė┌▀@Śl░ļÅĮĄ─ų▒ŠĆ╩ŪłAĄ─ŪąŠĆ.
ŪąŠĆ┼ąČ©│Żė├Ą─ūC├„ĘĮĘ©Ż║ó┘ų¬Ą└ų▒ŠĆ║═łAėą╣½╣▓³cĢr����Ż¼▀B░ļÅĮ����Ż¼ūC┤╣ų▒;ó┌▓╗ų¬Ą└ų▒ŠĆ┼cłAėąø]ėą╣½╣▓³cĢr���Ż¼ū„┤╣ų▒Ż¼ūC┤╣ŠĆČ╬Ą╚ė┌░ļÅĮ.
Ų▀��Īó╚²ĮŪą╬┼cłA
1.╚²ĮŪą╬Ą─═ŌĮėłAŽÓĻP(gu©Īn)Ė┼─Ņ
Įø(j©®ng)▀^╚²ĮŪą╬Ė„Ēö³cĄ─łAĮąū÷╚²ĮŪą╬Ą─═ŌĮėłA����Ż¼═ŌĮėłAĄ─łAą─Įąū÷╚²ĮŪą╬Ą─═Ōą─Ż¼▀@éĆ╚²ĮŪą╬Įąū÷łAĄ─ā╚(n©©i)Įė╚²ĮŪą╬.═Ōą─╩Ū╚²ĮŪą╬╚²Śl┤╣ų▒ŲĮĘųŠĆĄ─Į╗³c���Ż¼╦³ĄĮ╚²ĮŪą╬Ą─╚²éĆĒö³cĄ─ŠÓļxŽÓĄ╚.
2.╚²ĮŪą╬Ą─ā╚(n©©i)ŪąłA
┼c╚²ĮŪą╬Ė„▀ģČ╝ŽÓŪąĄ─łAĮąū÷╚²ĮŪą╬Ą─ā╚(n©©i)ŪąłA�Ż¼ā╚(n©©i)ŪąłAĄ─łAą─Įąū÷╚²ĮŪą╬Ą─ā╚(n©©i)ą─���Ż¼▀@éĆ╚²ĮŪą╬Įąū÷łAĄ─═ŌŪą╚²ĮŪą╬.ā╚(n©©i)ą─╩Ū╚²ĮŪą╬╚²ŚlĮŪŲĮĘųŠĆĄ─Į╗³c�Ż¼╦³ĄĮ╚²ĮŪą╬Ą─╚²Śl▀ģĄ─ŠÓļxŽÓĄ╚.
░╦�����Īóš²ČÓ▀ģą╬Ą─ėąĻP(gu©Īn)Ė┼─Ņ
š²ČÓ▀ģą╬ųąą─Ż║š²ČÓ▀ģą╬Ą─═ŌĮėłAĄ─łAą─Įąū÷▀@éĆš²ČÓ▀ģą╬Ą─ųąą─.
š²ČÓ▀ģą╬░ļÅĮŻ║š²ČÓ▀ģą╬═ŌĮėłAĄ─░ļÅĮĮąū÷š²ČÓ▀ģą╬░ļÅĮ.
š²ČÓ▀ģą╬ųąą─ĮŪŻ║š²ČÓ▀ģą╬├┐ę╗▀ģ╦∙ī”Ą─łAą─ĮŪĮąū÷š²ČÓ▀ģą╬ųąą─ĮŪ.
š²ČÓ▀ģą╬▀ģą─ŠÓŻ║š²ČÓ▀ģą╬ųąą─ĄĮš²ČÓ▀ģą╬Ą─ę╗▀ģĄ─ŠÓļxĮąū÷š²ČÓ▀ģą╬Ą─▀ģą─ŠÓ.
Š┼��Īó┼cłAėąĻP(gu©Īn)Ą─ėŗ╦Ń╣½╩Į
1.╗ĪķL║═╔╚ą╬├µĘeĄ─ėŗ╦ŃŻ║
╔╚ą╬Ą─╗ĪķL;
╔╚ą╬Ą─├µĘe.
2.łAÕF┼cé╚(c©©)├µš╣ķ_łD
1)łAÕFé╚(c©©)├µš╣ķ_łD╩Ūę╗éĆ╔╚ą╬Ż¼╔╚ą╬Ą─░ļÅĮĄ╚ė┌łAÕFĄ──ĖŠĆ����Ż¼╔╚ą╬Ą─╗ĪķLĄ╚ė┌łAÕFĄ─Ąū├µų▄ķL.
2)╚¶łAÕFĄ─Ąū├µ░ļÅĮ×ķrŻ¼─ĖŠĆķL×ķl����Ż¼ät▀@éĆ╔╚ą╬Ą─░ļÅĮ×ķlŻ¼╔╚ą╬Ą─╗ĪķL×ķ2πr�Ż¼
łAÕFĄ─é╚(c©©)├µĘe×ķSłAÕFé╚(c©©)=.
łAÕFĄ─▒Ē├µĘeŻ║SłAÕF▒Ē=SłAÕFé╚(c©©)+SłAÕFĄū=πrl+πr2=πr·(l+r).
į┌Ū¾▓╗ęÄ(gu©®)ätłDą╬Ą─├µĘeĢrŻ¼ūóęŌ└¹ė├ĖŅčaĘ©┼cĄ╚Ęeūā╗»ĘĮĘ©Üw×ķęÄ(gu©®)ätłDą╬����Ż¼į┘└¹ė├ęÄ(gu©®)ätłDą╬Ą─╣½╩ĮŪ¾ĮŌ.
į┌ųą┐╝ųąę╗░ŃĢ■į┌ĮŌ┤Ņ}╬╗ų├┐╝▓ķĄĮłAĄ─ŠC║ŽŅ}Ż¼╔µ╝░ĄĮłAĄ─ŽÓĻP(gu©Īn)ūC├„║═ėŗ╦Ń����Ż¼▀@ŅÉŅ}─┐▓╗āHāHĢ■┐╝▓ķĄĮłAĄ─ŽÓĻP(gu©Īn)ų¬ūR³c�����Ż¼▀ĆĢ■╔µ╝░ĄĮŲĮąąŠĆ�ĪóĄ╚č³╚²ĮŪą╬Īóų▒ĮŪ╚²ĮŪą╬�����Īó╚½Ą╚╚²ĮŪą╬ĪóŽÓ╦Ų╚²ĮŪą╬�Īó╚²ĮŪ║»öĄ(sh©┤)Īó╠ž╩Ō╦─▀ģą╬Ą╚ų¬ūR³c���Ż¼ėąę╗Č©Ą─ŠC║Žąį��ĪŻ
ŠÄ▌ŗ═Ų╦]Ż║
2023─Ļųą┐╝Ė„┐Ų─┐ųž³cų¬ūRģR┐é
ĪĪĪĪūŅą┬ųą┐╝┘YėŹ�Īóųą┐╝š■▓▀��Īó┐╝Ū░£╩éõ����Īóųą┐╝ŅA(y©┤)£yĪóõø╚ĪĘųöĄ(sh©┤)ŠĆĄ╚
ĪĪĪĪųą┐╝ĢrķgŠĆĄ─╚½▓┐ųžę¬╣Ø(ji©”)³c
ĪĪĪĪ▒Mį┌"ųą┐╝ŠW(w©Żng)"╬óą┼╣½▒Ŗ╠¢

ĪĪĪĪ ÜgėŁ╩╣ė├╩ųÖC����ĪóŲĮ░ÕĄ╚ęŲäėįO(sh©©)éõįLå¢ųą┐╝ŠW(w©Żng)Ż¼2023ųą┐╝ę╗┬Ę┼Ń░ķ═¼ąą�����ŻĪ>>³cō¶▓ķ┐┤











